Prüfen Sie Ihr Wissen!
- Kapitel 1: Deskriptive Statistik
- Kapitel 2: Inferenzstatistik
- Kapitel 3: Der t-Test
- Kapitel 4: Merkmalszusammenhänge
Aufgaben zu Kapitel 1: Deskriptive Statistik
Teil I: Verständnisaufgaben
Und so funktioniert es: Wenn Sie die Frage für sich beantwortet haben, markieren Sie einfach den Bereich unterhalb der jeweiligen Frage. Weiß auf blau finden Sie dort die richtige Antwort.
Aufgabe 1: Welche der folgenden Aussagen sind zutreffend?
a) Der Modalwert ist der Wert einer Verteilung, der die größte Auftretenswahrscheinlichkeit hat.
b) Wenn die Messwerte nur als ganze Zahlen vorliegen, muss der Median auch eine ganze Zahl sein.
c) Der Mittelwert ist formal definiert als die an der Anzahl der Messwerte relativierte Summe der Einzelwerte.
d) Es kann nur einen Modalwert geben.
e) Der Mittelwert liegt so, dass die Summe der quadrierten Abweichungen der Werte vom Mittelwert minimal ist.
f) Die Bestimmung des arithmetischen Mittels aus einer nominalskalierten Variablen ist inhaltlich sinnvoll.
g) Wird in einer Untersuchung die soziale Schicht der Versuchsperson erfasst, so kann es sich nur um eine nominalskalierte Größe handeln.
h) Auf Ordinalskalenniveau sind alle linearen Transformationen erlaubt.
Antwort: a, c, e und h.
Aufgabe 2: Bestimmen und diskutieren Sie die Skalentypen der folgenden Beispiele:
a) Postleitzahlen
b) Gewicht (kg), das ein Kind hochheben kann
c) Körperliche Verfassung, gemessen am Gewicht (kg), das ein Kind hochheben kann
d) Metrisches System zur Distanzmessung
e) Schulnoten
f) Intelligenz, gemessen an der Anzahl der Aufgaben in einem Test
Antworten:
a. Reines Klassifikationssystem, keine Informationen über Abstände und Reihenfolge; Skalentyp: Nominalskala.
b. Physikalische Skala mit Äquidistanz und definiertem Nullpunkt; Skalentyp: Verhältnisskala.
c. Enthält Informationen über eine Reihenfolge (je mehr das Kind heben kann, desto fitter ist es). Ob die relativen Abstände der körperlichen Verfassung allerdings korrekt durch Gewichtheben abgebildet werden, ist fraglich; Skalentyp: Ordinalskala.
d. Physikalische Skala mit Äquidistanz und definiertem Nullpunkt; Skalentyp: Verhältnisskala.
e. Vergleiche c.; mögliches Problem: unterschiedliche Aufgabenschwierigkeit; etablierte psychologische Intelligenztests liefern allerdings in den meisten Fällen intervallskalierte Daten.
f. In der Regel werden aus Schulnoten Mittelwerte gebildet, sie werden also als intervallskaliert betrachtet. Ob aber das Intervall zwischen 1 und 2 wirklich das Gleiche ist wie das zwischen 3 und 4, soll an dieser Stelle nur zur Diskussion anregen.
Teil II: Anwendungsaufgaben
Hier können Sie Ihr erworbenes Wissen anwenden und Beispiele berechnen. Die Lösungen zu den Anwendungsaufgaben im Kapitel 1 finden Sie hier, als Link zu einer pdf-Datei.
Aufgabe 1
Eine Lehrerin entnimmt dem Duden eine Zufallsstichprobe von 300 Wörtern der Alltagssprache, die sie ihren Schülern diktiert. Sie zählt anschließend bei jedem Schüler die Anzahl der richtig geschriebenen Worte und nennt diese Summe ein Maß für die »Allgemeine Rechtschreibfähigkeit«. Mit welchem Skalentyp können diese Daten dargestellt werden?
Aufgabe 2
Gegeben sind die Werte: 13; 28; 26; 19; 15; 16.
a. Ermitteln Sie das arithmetische Mittel, die Varianz und die Standardabweichung!
b. Transformieren Sie alle Werte nach der Gleichung y = 2x + 5 und wiederholen Sie Aufgabenteil a.
c. Überführen Sie die Werte in z-Werte.
Aufgabe 3
Die Messwerte zweier Gruppen sind wie in der nebenstehenden Tabelle angegeben.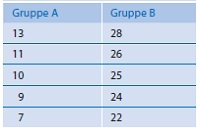
a. Berechnen Sie Mittelwerte und Varianzen der beiden Gruppen.
b. Berechnen Sie den Gesamtmittelwert und die Gesamtvarianz aller Personen.
Warum ist die Gesamtvarianz so groß?
Aufgabe 4
Eine Alters- und Geschlechtsumfrage, durchgeführt an 15 Studierenden der Pädagogik, liefert die Ergebnisse in dieser Tabelle rechts: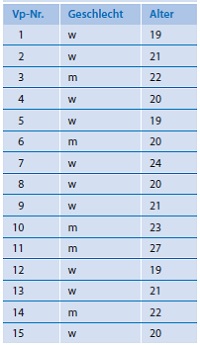
a. Welche Skalenqualitäten besitzen die beiden erhobenen Merkmale?
b. Berechnen Sie den Prozentanteil weiblicher und männlicher Versuchspersonen.
c. Fertigen Sie eine Häufigkeitstabelle für die Variable Alter an.
d. Ergänzen Sie die Tabelle aus c. um eine Prozentwerttabelle und eine kumulierte Prozentwerttabelle.
e. Wie viel Prozent der befragten Studierenden sind zwischen 19 und 21 Jahre alt?
f. Bestimmen Sie Median und Modus der Altersvariablen.
g. Berechnen Sie das Durchschnittsalter der Versuchspersonen.
h. Sind die Studentinnen im Durchschnitt älter oder jünger als die Studenten? Wie groß ist der Unterschied?
i. Bestimmen Sie Variationsbreite, Varianz und Streuung der Altersverteilung.
Aufgabe 5
Eine Versuchsperson erhält in einem Angsttest (μ = 20, σ2 = 25) den Testwert 12. Welches Ergebnis würde sie theoretisch in einem anderen Angsttest mit μ = 0 und σ2 = 100 erreichen?
Aufgaben zu Kapitel 2: Inferenzstatistik
Teil I: Verständnisaufgaben
Und so funktioniert es: Wenn Sie die Frage für sich beantwortet haben, markieren Sie einfach den Bereich unterhalb der jeweiligen Frage. Weiß auf blau finden Sie dort die richtige Antwort.
Aufgabe 1
Wie viele und welche Merkmale sind nötig, um eine Normalverteilung vollständig zu beschreiben?
Antwort: Zwei: Mittelwert und Streuung.
Aufgabe 2
In zwei Untertests eines Intelligenz-Struktur-Tests erzielt Mario die Werte x1 = 12 und x2 = 23. Hat Mario in beiden Tests »gleich gut« abgeschnitten? - Gegebene Werte: μ 1 = 10; μ2 = 20 ; σ 1 = 2; σ 2 = 3
Antwort: Beide Punktwerte liegen eine Standardabweichungseinheit über dem Mittelwert. Da beide Tests hinreichend normalverteilt sind, hat Mario in beiden Tests den gleichen Prozentrang und ist somit in beiden Tests »gleich gut«.
Aufgabe 3
Ein Test für Extraversion hat den Populationsmittelwert von μ = 15 und eine Populationsstreuung von σ = 2.
a) Wie groß ist die Wahrscheinlichkeit, dass eine Versuchsperson in diesem Test einen Wert von 10 oder weniger bekommt?
b) Wie wahrscheinlich ist es, dass eine Versuchsperson einen Wert zwischen 13 und 17 erhält?
c) Ab welchem Wert kann man jemanden als außergewöhnlich extravertiert bezeichnen?
d) Ab welchem Mittelwert kann man eine Gruppe von 4 Leuten als außergewöhnlich extravertiert bezeichnen?
Antworten:
a) Z-Transformation eines einzelnen Wertes: z = (xi -- μ) / σx = (10 -- 15) / 2 = 2,5. Das heißt, die Wahrscheinlichkeit p für einen Wert gleich 10 oder einen kleineren Wert beträgt p = 0,0062 = 0,62% (siehe z-Werte-Tabelle).
b) Der Bereich 13 bis 17 entspricht in diesem Test ± einer Standardabweichung. Die Wahrscheinlichkeit, dass eine Versuchsperson einen Wert zwischen 13 und 17 erhält, ist p = 0,68 (68 %).
c) Wir könnten z. B. festlegen, jemanden als außergewöhnlich extravertiert zu bezeichnen, wenn sein Wert mindestens zwei Streuungseinheiten (SE) über dem Mittelwert liegt. Bei einer Streuung von zwei und einem Populationsmittelwert von 15 wäre eine Versuchsperson ab einem Extraversionswert von 19 außergewöhnlich extravertiert.
d) Wir könnten auch hier einen Abstand von zwei Streuungseinheiten festlegen, um »außergewöhnlich extravertiert« zu spezifizieren. Allerdings wird die Streuung von Mittelwerten durch den Standardfehler bestimmt (siehe Formel auf Seite 26 im Kapitel 2 → Link "Probekapitel"). Bei einem Standardfehler von 1 und einem Populationsmittelwert von 15 würde man eine Gruppe von 4 Personen ab einem Gruppenmittelwert von 17 als außergewöhnlich extravertiert bezeichnen.
Teil II: Verständnisaufgaben
Hier können Sie Ihr erworbenes Wissen anwenden und Beispiele berechnen. Um die Lösungen der Anwendungsaufgaben zu sehen, markieren Sie einfach den Bereich unter der Aufgabenstellung. Dort erscheint dann die richtige Antwort weiß auf blau.
Aufgabe 1
Bestimmen Sie den z-Wert einer Standardnormalverteilung,
a) oberhalb dessen 20 Prozent der Werte liegen.
b) unterhalb dessen 65 Prozent der Werte liegen.
Antwort:
a) Oberhalb von z = 0,84 liegen 20 % der Werte
b) Unterhalb von z = 0,39 liegen 65 % der Werte
Aufgabe 2
Bestimmen Sie, wie viel Prozent der Fälle bei einer Normalverteilung und bei einer Standardnormalverteilung in dem Bereich »Mittelwert ± 1,5 Standardabweichungseinheiten« liegen.
Antwort: Bei beiden Verteilungen liegen 86,6 % der Fläche zwischen ±1,5 Standardabweichungseinheiten. In der z-Tabelle sind die Flächen angegeben, die der jeweilige z-Wert nach links abschneidet. Bei der Berechnung der Fläche zwischen zwei Grenzen müssen wir die Fläche der unteren Grenze von der Fläche der oberen Grenze abziehen. Für z = –1,5 und z = +1,5 also: 0,9332 – 0,0668 = 0,8664
Aufgabe 3
Ein Firmenchef möchte nur sehr intelligente Bewerber einstellen, nämlich nur solche, die in den oberen 5 % der Population liegen. Wie groß muss der IQ-Wert einer Person in einem Intelligenztest mindestens sein, um bei ihm einen Job zu bekommen?
(Intelligenztest: μ = 100, σ = 15)
Antwort: Die Frage ist, wie groß der IQ-Wert ist, der 5 % der Fläche in der Häufigkeitsverteilung nach rechts abschneidet? Rechenweg: Den z-Wert nachschlagen, der 95 % der Fläche nach links abschneidet, und diesen z-Wert in die Verteilung des Intelligenztests transformieren.
p = 0,95 ⇒ z = 1,65
x = σx · zx + μ = 15 · 1,65 + 100 = 124, 75
Eine Person müsste also mindestens einen IQ von 125 haben, um in dieser Firma einen Job zu bekommen.
Aufgaben zu Kapitel 3: Der t-Test
Teil I: Verständnisaufgaben
Und so funktioniert es:Wenn Sie die Frage für sich beantwortet haben, markieren Sie einfach den Bereich unterhalb der jeweiligen Frage. Weiß auf blau finden Sie dort die richtige Antwort.
Aufgabe 1
Beantworten Sie folgende Fragen:
a. Wie lauten – jeweils in einem Satz – die Annahmen der Nullhypothese und der Alternativhypothese?
b. Wodurch unterscheidet sich die ebenfalls standardisierte t-Verteilung von der z-Verteilung?
c. Wozu dient die Festlegung eines Signifikanzniveaus?
d. Was sind die mathematischen Voraussetzungen für die Anwendung eines t-Tests?
e. Was ist der Unterschied zwischen einer ungerichteten und einer gerichteten Alternativhypothese?
f. Was ist der Varianzquotient Ω2?
Antworten:
a) Nullhypothese: Die Ursache für die Differenz zwischen den Mittelwerten zweier untersuchter Gruppen ist rein zufällig zustande gekommen, d. h., die beiden Stichproben wurden aus zwei Populationen gezogen, die denselben Populationsmittelwert und dieselbe Streuung haben. Alternativhypothese: Es besteht ein systematischer Unterschied zwischen den beiden untersuchten Gruppen, d. h., die beiden Stichproben wurden aus Populationen gezogen, die einen unterschiedlichen Populationsmittelwert haben.
b) Die t-Verteilung ist trotz der Standardisierung immer noch von dem Stichprobenumfang abhängig. Dies liegt daran, dass in die Berechnung des t-Werts nicht einer, sondern zwei erwartungstreue Schätzer für Populationsparameter eingehen: Es müssen die Varianzen von zwei Populationen geschätzt werden, um die Streuung der Stichprobenkennwerteverteilung selbst zu schätzen. Die Freiheitsgrade der gefundenen Mittelwertsdifferenz erlauben eine genaue Beschreibung der zu verwendenden t-Verteilung.
c) Mit der Festlegung eines Signifikanzniveaus wird ein Entscheidungskriterium für die Bewertung des empirischen Ergebnisses bestimmt. Ist die uftretenswahrscheinlichkeit des empirischen Ergebnisses unter der Nullhypothese kleiner als das gewählte Signifikanzniveau, so wird die Nullhypothese abgelehnt und die Alternativhypothese angenommen.
d) Die mathematischen Voraussetzungen für den t-Test sind die Intervallskalenqualität der Messdaten, die Normalverteilung des untersuchten Merkmals in der Population und die Varianzhomogenität (Gleichheit der Varianzen) der Populationen der beiden Stichproben.
e) Eine ungerichtete Alternativhypothese nimmt lediglich an, dass die Differenz der Populationsmittelwerte nicht gleich null ist. Eine gerichtete Alternativhypothese sagt bereits eine erwartete Richtung der Mittelwertsdifferenz voraus.
f) Der Varianzquotient Ω2 ist ein prozentuales Effektstärkenmaß. Er bestimmt das Verhältnis der systematischen Varianz zur Gesamtvarianz.
Aufgabe 2
Beschreiben Sie …
a. den α-Fehler.
b. den β-Fehler.
c. den Zusammenhang zwischen dem β-Fehler und der Teststärke.
d. die gegenseitige Abhängigkeit der Fehlerwahrscheinlichkeiten.
Antworten:
a) Der α-Fehler oder Fehler 1. Art ist die Entscheidung für die H1, obwohl in Wirklichkeit die H0 gilt. Die α-Fehlerwahrscheinlichkeit ist α = p(H1|H0).
b) Der β- Fehler oder Fehler 2. Art ist die Entscheidung für die H0, obwohl in Wirklichkeit die H1 gilt. Die β-Fehlerwahrscheinlichkeit ist β = p(H1|H0).
c) Die Teststärke ist gleich 1 – β.
d) Nach Bestimmung eines Signifikanzniveaus α ist die β-Fehlerwahrscheinlichkeit festgelegt, wenn die Stichprobengröße und der angenommene Effekt nicht verändert werden. Eine Verkleinerung von α bedingt dann eine Vergrößerung von β und damit eine Verkleinerung der Teststärke. Es ist deshalb nicht immer sinnvoll, in einem t-Test ein sehr niedriges Signifikanzniveau zu wählen, weil durch den größeren β-Fehler ein nicht signifikantes Ergebnis nicht mehr eindeutig zu interpretieren sein kann.
Aufgabe 3
Ergänzen Sie die fehlenden Satzteile im nachfolgenden Text (bei kursiv geschriebenen Worten ist die falsche Alternative zu streichen)!
Der β-Fehler ist die Wahrscheinlichkeit, sich fälschlicherweise (a) für /gegen die Alternativhypothese zu entscheiden. Um den β-Fehler zu erhalten, muss man zunächst eine(n) (b) ____ festlegen. Je weniger Versuchspersonen man erhebt, desto (c) ___ wird der β-Fehler bei sonst gleichen Größen, denn umso (d) ___ wird auch die Streuung der (e) ___ -verteilung. Je größer der interessierende Populationseffekt ist, desto (f) ___ wird die Teststärke. Die Teststärke gibt die Wahrscheinlichkeit an, mit der man ein signifikantes Ergebnis (g) findet / nicht findet, falls ein Populationseffekt einer bestimmten Größe (f) existiert/nicht existiert. Auch das α-Niveau spielt hier eine Rolle, denn je strenger man dieses festlegt, desto (h) ___ wird die Teststärke.
Antworten:
a) gegen
b) Populationseffekt
c) größer
d) größer
e) Stichprobenkennwerte-
f) größer
g) findet
h) kleiner
Teil II: Anwendungsaufgaben
Hier können Sie Ihr erworbenes Wissen anwenden und Beispiele berechnen. Die Lösungen zu den Anwendungsaufgaben finden Sie hier als Link zu einer pdf-Datei..
Aufgabe 1
Ein Persönlichkeitspsychologe glaubt, dass die Leistung in einem Intelligenztest steigt, wenn man die Versuchspersonen für richtige Antworten belohnt. Um diese Hypothese zu überprüfen, führt er eine Untersuchung mit 60 Personen durch: Der einen Hälfte (n1 = 30) verspricht er für jede gelöste Aufgabe im Intelligenztest 1 Euro Belohnung (der Test umfasst 50 Aufgaben), die andere Hälfte (n2 = 30) erhält keine Belohnung für gelöste Aufgaben. Die Mittelwerte der jeweils erreichten Gesamtpunktzahl sollen mit einem t-Test für unabhängige Stichproben verglichen werden.
a. Muss hier ein ein- oder ein zweiseitiger Test durchgeführt werden?
b. Welche statistische Hypothese ist relevant für die inhaltliche Fragestellung?
c. Wenn die Annahme des Psychologen stimmt, müsste die empirische Mittelwertsdifferenz (x 1 − x2) dann eher positiv, negativ oder null sein?
d. Wie würde sich die Streuung der Stichprobenkennwerteverteilung verändern, wenn der Psychologe den Test mit n1 = n2 = 40 durchgeführt hätte?
Aufgabe 2
In der Klinik für Psychosomatik in H. wurde kürzlich eine Therapie zur Linderung von Migräne entwickelt, die im Gegensatz zu herkömmlichen Therapien mehr als 10 % der angesetzten Behandlungsstunden einspart. Nun soll der Erfolg der Therapie mittels eines speziell dafür entwickelten Messinstruments, das intervallskalierte Daten liefert, untersucht werden. Die Entwickler der neuen Therapie glauben, dass der Therapieerfolg trotz der kürzeren Behandlungszeit der gleiche ist.
a. Welcher statistische Kennwert wird hier auf Signifikanz geprüft (bitte genau angeben)?
b. Welchen Wert sollte dieser Kennwert gemäß der inhaltlichen Hypothese der Entwickler in der Population haben?
Aufgabe 3
Ein Soziologe führt ein Experiment durch (zwei unabhängige Gruppen, n1 = n2 = 65), in dem die inhaltliche Hypothese mit der Alternativhypothese des statistischen Tests verknüpft ist und besagt: μ1 – μ2 > 0. Er findet eine Mittelwertsdifferenz von x 1 − x2 = −26 . Die geschätzten Populationsstreuungen betragen σ1 = 290 und σ2 = 280. Welchen Schluss kann der Soziologe aufgrund seines empirischen Ergebnisses ziehen?
Aufgabe 4
Eine Psychologiestudentin möchte, dass die Versuchspersonen nach der Teilnahme an ihren Experimenten glücklich und zufrieden sind. Sie will ihnen deshalb eine Belohnung für die Teilnahme zukommen lassen. Aber wie viel? Hängt die Zufriedenheit überhaupt von der Höhe der Belohnung ab? Sie beschließt, diese Frage an einigen Versuchspersonen zu untersuchen. Ihre Ergebnisse stehen in der Tabelle. Höhere Werte zeigen eine höhere Zufriedenheit an.
a. Berechnen Sie Mittelwerte und Streuungen.
b. Ist das Ergebnis signifikant?
Aufgabe 5
Ein Sozialpsychologe möchte die Stimmung von Versuchspersonen mit Filmen beeinflussen. Er zeigt den Versuchspersonen entweder Ausschnitte aus einem traurigen Film (»Schindlers Liste«) oder einem lustigen Film (»Die Nackte Kanone 2½«) und lässt sie dann auf einer 9-stufigen Skala ihre Stimmung angeben (Intervallskalenniveau). Der Forscher nimmt an, dass ein lustiger Film im Vergleich zu einem traurigen Film die Stimmung hebt.
a. Gibt es einen Einfluss der Filme auf die Stimmung?
b. Wie groß ist dieser Einfluss?
c. Wie viele Personen hätte der Forscher untersuchen müssen, um einen Populationseffekt der Größe Ω2 = 0,05 mit 90 %iger Wahrscheinlichkeit zu finden?
➫ Ergebnisse:
x positiv = 6.8; σ2pos = 3.2; npos = 25
x negativ = 5.9; σ2neg = 3.8; nneg = 28
Aufgabe 6
In einer Zweigruppen-Untersuchung wird die Mittelwertsdifferenz auf Signifikanz getestet. Dabei erhält man einen t-Wert von t (df = 158) = 4,88.
a. Welche statistische Entscheidung fällt man, wenn das α-Niveau 5 % beträgt (ungerichtete Fragestellung)?
b. Welche inhaltliche Entscheidung fällt man, wenn der mindestens interessierende Populationseffekt Ω2 ≥ 0,1 betragen soll?
Aufgabe 7
Eine Entwicklungspsychologin will überprüfen, ob das Körpergewicht einer Person auch einem genetischen Einfluss unterliegt. Dazu untersucht sie 21 Zwillingspaare (eineiig; Gruppe 1) und 21 »normale« gleichgeschlechtliche Geschwisterpaare (Nicht-Zwillinge; Gruppe 2) und bildet für jedes Paar die »Gewichtsdifferenz« ΔG. Anschließend mittelt sie diese Werte pro Gruppe und testet die Differenz der beiden so entstandenen Gruppenmittelwerte auf Signifikanz. Ihre Hypothese lautet: "Die Gewichtsdifferenz ist bei eineiigen Zwillingen kleiner (d. h., die Körpergewichte der Geschwister sind ähnlicher) als bei Nicht-Zwillingen".
➫ Ergebnisse:
Zwillingspaare: durchschnittliches ΔG(1) = 2855 g / Streuung: σ1 = 780 g
Nicht-Zwillinge: durchschnittliches ΔG(2) = 4012 g / Streuung: σ2 = 820 g
Mit diesen Werten rechnet sie einen t-Test für unabhängige Stichproben.
a. Wie lautet das formale statistische Hypothesenpaar dieses Tests und welche der Hypothesen ist mit der inhaltlichen Fragestellung verknüpft?
b. Rechnen Sie den entsprechenden t-Test (sinnvolles Runden ist erlaubt)!
c. Zu welchem Ergebnis kommen Sie und warum (α = 0,05)?
Aufgabe 8
In einem Gedächtnisexperiment mit zwei Gruppen wird die Mittelwertsdifferenz auf Signifikanz geprüft. Man erhält einen t-Wert von t(df=132) = 3,2 (einseitiger Test; signifikant auf dem 5%-Niveau). Wie groß ist die empirische Effektgröße?
Aufgabe 9
Ein Wissenschaftler erhält in einem Zweigruppen-Experiment einen empirischen t- Wert von t(df=60) = 1,4. Dieser Wert ist auf einem 5%-α-Niveau (einseitig) nicht signifikant. Er legt fest, dass der Populationseffekt mindestens Ω2 ≥ 0,2 betragen sollte, um inhaltlich bedeutsam zu sein.
a. Wenn er sich schon nicht für die H1 entscheiden kann: Was muss der Wissenschaftler tun, um sich eventuell für die H0 zu entscheiden? (bitte ausführliche Rechnung)
b. Beurteilen Sie das Ergebnis.
c. Wie würde sich das Ergebnis dieses Tests verändern, wenn der Wissenschaftler einen Populationseffekt von Ω2 ≥ 0,4 angenommen hätte? (nicht rechnen)
d. Wie würde sich das Ergebnis verändern, wenn der Forscher ein α-Niveau von 10 % akzeptiert hätte?
Aufgabe 10
Ein zweiseitiger t-Test wird entgegen der Annahmen des Wissenschaftlers auf dem 5%-Niveau nicht signifikant. Der Forscher hat den Verdacht, dass dieses Ergebnis vielleicht aufgrund seines geringen Stichprobenumfangs zustande gekommen sein könnte. Wie viele Versuchspersonen hätte der Forscher insgesamt untersuchen müssen, um mit 95%-iger Wahrscheinlichkeit ein signifikantes Ergebnis zu erhalten, wenn er davon ausgeht, dass der Effekt in der Population mindestens Ω2 ≥ 0,15 beträgt?
Aufgabe 11
Eine Forscherin führt mit einer gefundenen Mittelwertsdifferenz (n1 = n2 = 40) einen zweiseitigen t-Test durch, wobei die inhaltliche Hypothese mit der statistischen Nullhypothese verknüpft ist. Der Test wird erwartungsgemäß nicht signifikant (α-Niveau: 1 %). Die Forscherin legt nun fest, dass der Effekt in der Population maximal 5 % betragen darf, um die Nullhypothese nicht zu verletzen. Wenn der Effekt tatsächlich Ω2 ≤ 0,05 betragen würde, wie groß ist dann die Teststärke?
Aufgabe 12
Ein Forscher hat die Wirksamkeit eines neuen Medikaments untersucht. Dafür hat er die Linderung der Krankheit durch das Medikament mit einem Placebo verglichen. Er erhält ein signifikantes Ergebnis mit t(df=298) =1,96 und bietet den Ärzten nun sein Medikament zum Kauf an. Ein Freund von Ihnen ist Arzt und überlegt, ob er das angebotene Medikament verwenden soll. Was können Sie Ihrem Freund empfehlen?
Aufgabe 13
Ein Therapeut behauptet, dass eine von ihm entwickelte Meditation die Zufriedenheit von Menschen positiv beeinflusst. Er möchte dies mit wissenschaftlichen Methoden zeigen und misst die Zufriedenheit vor und nach der Meditation (Daten mit Intervallskalenqualität). Es ergeben sich die Werte in der nebenstehenden Tabelle.
a. Stellen Sie die statistischen Hypothesen auf.
b. Berechnen Sie den Kennwert des Tests und seine Streuung.
c. Führen Sie einen t-Test durch. Wirkt die Meditation auf die Zufriedenheit?
Aufgaben zu Kapitel 4: Merkmalszusammenhänge
Teil I: Verständnisaufgaben
Und so funktioniert es: Wenn Sie die Frage für sich beantwortet haben, markieren Sie einfach den Bereich unterhalb der jeweiligen Frage. Weiß auf blau finden Sie dort die richtige Antwort.
Aufgabe 1
Erklären Sie, wodurch jeweils ein positiver, negativer oder kein Zusammenhang zwischen zwei Variablen zustande kommt. Geben Sie für jeden der drei Fälle ein Beispiel.
Antwort:
Ein positiver Zusammenhang bedeutet, dass die Werte auf beiden Variablen in gleicher Weise variieren (vom Mittelwert abweichen), d. h. überdurchschnittliche Werte auf x entsprechen überdurchschnittlichen Werten auf y, während unterdurchschnittliche Werte auf x mit unterdurchschnittlichen Werten auf y einhergehen.
Beispiel: Aufmerksamkeit und Erinnerung. Ein negativer Zusammenhang tritt auf, wenn hohe Werte auf der einen Variable mit niedrigen Werten auf der anderen einhergehen und umgekehrt. Beispiel: Angst und Selbstsicherheit. Kein Zusammenhang existiert, wenn beide Variablen unsystematisch miteinander variieren, d. h., es lässt sich kein Trend feststellen. Beispiel: Schuhgröße und Introversion.
Aufgabe 2
Wie ist der Korrelationskoeffizient rxy definiert? Welche Vorteile hat er als deskriptives Maß gegenüber der Kovarianz?
Antwort:
Der Korrelationskoeffizient ist der Quotient aus empirischer Kovarianz und maximaler Kovarianz. Die maximale Kovarianz entspricht dem Produkt der beiden Merkmalsstreuungen. Der Korrelationskoeffizient ist aufgrund der Relativierung maßstabsunabhängig (standardisiert) und hat einen festen Wertebereich 1 bis +1). Korrelationskoeffizienten unterschiedlicher Stichproben oder verschiedener Variablen können so miteinander verglichen werden, was mit der Kovarianz nicht möglich ist.
Aufgabe 3
Was besagt eine Kovarianz/Korrelation von null?
Antwort:
Eine Kovarianz (Korrelation) von null besagt, dass die untersuchten Merkmale voneinander unabhängig sind, d. h., Variable x steht in keinerlei Zusammenhang mit Variable y.
Aufgabe 4
Wie führt man eine arithmetische Mittelung von Korrelationskoeffizienten durch? Nennen Sie die wesentlichen Schritte.
Antwort:
Mithilfe der Fishers Z-Transformation lassen sich Produkt-Moment-Korrelationen mitteln. Die nötigen Schritte sind:
1. Transformation der einzelnen Werte in Fishers Z-Werte
2. Bilden eines Z-Mittelwerts
3. Rücktransformation des Z-Mittelwerts in eine Korrelation
Aufgabe 5
Bringen Sie die Begriffe lineare Regression, Kriterium, Prädiktor, Regressionsgleichung, abhängige Variable und unabhängige Variable in einen sinnvollen Zusammenhang!
Antwort:
Die lineare Regression dient der Merkmalsvorhersage. Aus der Ausprägung der unabhängigen Variable x, genannt Prädiktor, kann die zugehörige Ausprägung der abhängigen Variable, des Kriteriums, mithilfe der Regressionsgleichung vorhergesagt werden.
Aufgabe 6
Welche Aussage gestattet der Determinationskoeffizient?
Antwort:
Der Determinationskoeffizient gibt denjenigen Varianzanteil der abhängigen Variable y wieder, der durch die unabhängige Variable aufgeklärt werden kann. Er ist somit ein prozentuales Maß für den gemeinsamen Varianzanteil zweier Variablen. Ebenso lässt er sich als Effektstärkenmaß begreifen, das die Größe des Einflusses der unabhängigen Variable auf die abhängige Variable angibt.
Aufgabe 7
Welche Beziehung besteht bei der linearen Regression zwischen der Gesamtvarianz, der Regressionsvarianz und der Residualvarianz?
Antwort:
Bei der linearen Regression lässt sich die Gesamtvarianz der tatsächlichen Werte des Kriteriums in die Regressionsvarianz und die Residualvarianz aufspalten: (Gesamtvarianz)2 = (Regressionsvarianz)2 + (Residualvarianz)2
Teil II: Anwendungsaufgaben
Hier können Sie Ihr erworbenes Wissen anwenden und Beispiele berechnen. Die Lösungen zu den Anwendungsaufgaben von Kapitel 4 finden Sie hier als Link zu einer pdf-Datei..
Aufgabe 1
An 15 Pädagogikstudenten wurden die Punktwerte in zwei Tests zur Erfassung von Hilfsbereitschaft erhoben. Dabei bedeuten hohe Werte im jeweiligen Test eine hohe Ausprägung an prosozialem Verhalten.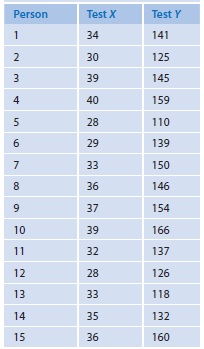
a. Zeichnen Sie ein Streudiagramm der Daten. Welche Art von Zusammenhang lässt sich vermuten?
b. Bestimmen Sie die Kovarianz zwischen den beiden Tests.
c. Berechnen Sie die Produkt-Moment-Korrelation rxy.
Aufgabe 2
In einem Datensatz sind σ x = 3 und σ y = 7.
a. Welchen Wert kann die Kovarianz zwischen den beiden Merkmalen maximal annehmen?
b. Wie hoch müsste die empirische Kovarianz zwischen den Variablen mindestens sein, damit sich eine Korrelation von über 0,80 ergibt?
Aufgabe 3
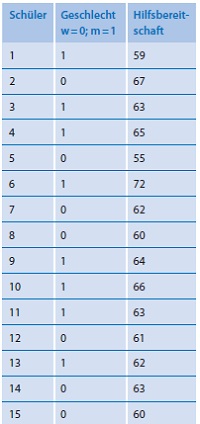Sie sollen in einer Studie klären, ob es innerhalb einer bestimmten Klasse einen Zusammenhang zwischen dem Geschlecht der Schüler und deren Hilfsbereitschaft gibt. Diese wird mithilfe eines speziellen Tests mit Intervallskalenqualität erhoben. Ihre Untersuchung erbrachte die Daten in nebenstehender Tabelle.
a. Bestimmen Sie die Güte des Zusammenhangs der untersuchten Variablen.
b. Ist das gefundene Ergebnis statistisch signifikant (α = 0,05)?
Aufgabe 4
Ein Weinhersteller wirbt Kunden mit dem Argument, dass Rotweinkonsum Weisheit fördere, da Rotweinkonsum und Weisheit zu r = 0,45 korreliert sind. Ein Psychologe bezweifelt dies, da beide Variablen mit dem Alter zusammenhängen: Rotweinkonsum und Alter zu r = 0,68, Weisheit und Alter zu r = 0,55. Zeigen Sie, dass der Weinhersteller einer Scheinkorrelation auf den Leim gegangen ist!
Aufgabe 5
Zwölf Studierende werden anhand ihrer Ergebnisse in einer Statistikklausur in eine Rangreihe gebracht. Dem Besten wurde Rang 1 zugeteilt, dem Zweiten Rang 2 usw. Dieselben Studenten unterzogen sich einem Intelligenztest und wurden anschließend ebenfalls anhand der Ergebnisse in eine Reihenfolge vergleichbar der ersten eingeteilt. Diese beiden Rangfolgen sind in der Tabelle aufgeführt. Berechnen Sie die Korrelation der beiden Rangfolgen nach Spearman.
Aufgabe 6
In der Persönlichkeitsforschung betrifft eine kontroverse Frage den Anteil, den die Vererbung an der Ausprägung von Persönlichkeitsmerkmalen hat wie z. B. der Intelligenz. Ein wichtiges Untersuchungsparadigma ist die Zwillingsforschung. In dem Maße, in dem sich getrennt voneinander aufgewachsene eineiige Zwillinge bezüglich eines Merkmals ähnlich sind, kann auf eine genetische Veranlagung des Merkmals geschlossen werden. Zehn getrennt voneinander aufgewachsene (eineiige) Zwillingspaare nehmen in einer Studie an einem Intelligenztest teil. Die Ergebnisse des Tests zeigt nebenstehende Tabelle.
a. Zeichnen Sie die Verteilung der Messwertepaare in ein Koordinatensystem ein (x-Achse: Zwilling 1; y-Achse: Zwilling 2).
b. Bestimmen Sie diejenige lineare Funktion, die es erlaubt, die Merkmalsausprägung y aus den Werten von x vorherzusagen.
c. Zeichnen Sie die zugehörige Regressionsgerade in das Koordinatensystem ein.
d. Bestimmen Sie die Residualvarianz und den Standardschätzfehler der linearen Regression.
e. Geben Sie eine statistisch fundierte Antwort auf die Frage nach dem Anteil, den die Anlage (Vererbung) in diesem Beispiel an der Ausprägung von Intelligenz hat. Welchen Einfluss repräsentiert die Residualvarianz?
Aufgabe 7
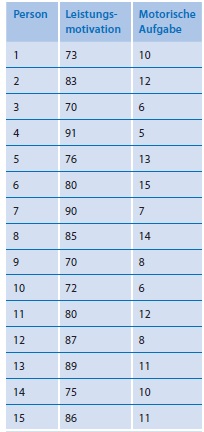Es soll untersucht werden, in welchem Zusammenhang die in einem Test erfasste Leistungsmotivation mit der Leistung in einer motorischen Geschicklichkeitsaufgabe steht. Für die 15 Testpersonen wurden die angeführten Daten ermittelt (siehe Tabelle links)
a. Zeichnen Sie das Streudiagramm.
b. Berechnen Sie rxy.
c. Diskutieren Sie die Höhe des Korrelationskoeffizienten und die Art des Zusammenhangs.
Aufgabe 8
Eine Persönlichkeitspsychologin interessiert sich für den Zusammenhang von Angstneigung und Kreativität. Die Angstneigung wird dabei über einen Test (normiert mit Mittelwert 50 und Streuung 10) erfasst, die Kreativität hingegen so, dass der Proband zu einem vorgegebenen Bild möglichst viele Assoziationen aufschreiben soll. Die Psychologin erhält die Ergebnisse in der Tabelle.
a. Erstellen Sie ein Streudiagramm der beiden interessierenden Variablen (x-Achse: Assoziationen; y-Achse: Testwert). Was können Sie über Richtung und Stärke des Zusammenhangs bereits jetzt aussagen?
b. Berechnen Sie die univariaten Statistiken der beiden Variablen (Mittelwerte, Varianzen und Streuungen).
c. Berechnen Sie die Kovarianz der beiden Variablen.
d. Berechnen Sie den Korrelationskoeffizienten.
e. Nehmen wir an, die Psychologin will Angsttestwerte aus der Anzahl der Assoziationen vorhersagen. Wie muss sie prinzipiell vorgehen? (nicht rechnen, nur beschreiben)
f. Berechnen Sie die Regressionsgleichung und zeichnen Sie die dazugehörige Gerade in das Streudiagramm ein.
g. Berechnen Sie den Determinationskoeffizienten. Was sagt er aus?
h. Berechnen Sie den Standardschätzfehler der Regression.
i. Wie groß ist die Regressionsvarianz?
j. Wie hoch wäre der Korrelationskoeffizient, wenn die Angstwerte der Prädiktor wären und die Anzahl der Assoziationen das Kriterium?
k. In welchem konkreten Punkt schneiden sich die beiden möglichen Regressionsgeraden?
l. In zwei anderen Studien wurden mit dem gleichen Vorgehen Korrelationen zwischen Angst und Assoziation von r = –0,70 und r = –0,62 gefunden. Errechnen Sie zusammen mit dem hier gefundenen Ergebnis eine mittlere Korrelation!
m. Wie groß ist die Korrelation zwischen dem Alter der Versuchspersonen und ihren Angstwerten?
n. Berechnen Sie aus der Prädiktorvariable »Alter« den vorhergesagten Wert im Angsttest für eine Versuchsperson, die a) 18 Jahre, b) 40 Jahre und c) 100 Jahre alt ist. Beurteilen Sie anhand eines geeigneten Maßes, ob diese Vorhersage sinnvoll ist. Wenn man für diese Regression (Alter und Angst) die Gerade in das entsprechende Streudiagramm einzeichnet, wie groß kann maximal die Steigung dieser Geraden werden? Wie groß ist die maximale Steigung dieser Geraden, wenn man die Variablen vorher z-standardisiert?
o. Berechnen Sie den geeigneten Korrelationskoeffizienten für den Zusammenhang zwischen dem Geschlecht der Versuchsperson und ihren Werten im Angsttest!
p. Wie viel Prozent der Varianz der Angstwerte wird durch die Variable »Geschlecht der Versuchsperson« aufgeklärt?
q. Ein anderer Psychologe führt die Untersuchung zum Zusammenhang von »Angstneigung« und »Kreativität« nochmals durch, diesmal allerdings (schlauerweise) mit viel mehr Versuchspersonen. Die Kreativität erfasst er über eine Selbsteinschätzung der Personen: Sie sollen angeben, ob sie sich für »eher kreativ« oder »eher nicht kreativ« halten. Welcher Korrelationskoeffizient muss hier gewählt werden?